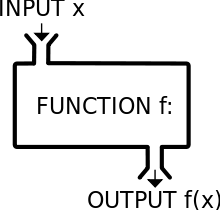
Function Notation
Function notation is just a fancy way of saying 'y'. The letter before the parenthesis names the function. The letter inside the parenthesis is the variable that you will be plugging in.
Function notation is just a fancy way of saying 'y'. The letter before the parenthesis names the function. The letter inside the parenthesis is the variable that you will be plugging in.
|
Domain
1 2 3 4 5 |
Range
4 8 12 16 20 |
This is an example of a function because each input has exactly ONE output. |
|
Domain
1 2 3 4 2 |
Range
1 3 6 3 6 |
This is an example of a set of domain and range that is NOT a function. Every input does NOT have exactly one output. |
Real World Function Notation
Linear
The Putnam County High School's Books and Breakfast Club is having it's annual Book-A-Thon. The library has put out a list of a total of one hundred books that they see fit for teens. Who ever reads the most books on the list will win a mystery prize. Jessie, and avid reader, is planning on beating the pulp out of her fellow contestees by reading the most books. She has already viewed the list, and has realized that she has already read ten of the books. She decides to pace herself by reading two books per week.
_Write a linear function using function notation to represent the situation.
b(x)=2x+10
Since this function is about books, it would be suitable to represent the function by b. The 2 represents how many books she reads per week(x). This would be the slope if we were to graph this function. The 10 represents the books she has already read. This would be the y-intercept if we were to graph the function.
_ Evaluate the function for inputs in the domain based on the context of the scenario.
Based on the context of the scenario, the number of weeks is substituted for x. Lets say Jessie wanted to know how many books she would have read in 10 weeks. We would plug in 10 to the function:
b(x)=2x+10
b(10)=2(10)+10
b(10)=20+10
b(10)=30
By plugging in ten to the function, Jessie now knows that she will have read 30 books from the list by the end of the 10th week. She can now figure out how many books she would have read in any number of weeks (x).
_Write a recursive formula for this scenario.
t1=12
tn=tn-1 + 2
Exponential
Summer, another member of the Books and Breakfast Club, is also planning on participating in the Book-A-Thon. She has heard about Jessie's scheme, and plans on beating her to the prize. She will stop at no ends to crush Jessie. Summer plans on reading 50 pages the first week, and doubling the amount each week. Although Summer has not yet read any of the books on the list, she plans on slowly, but surely, crawling her way to 1st place.
_Write an exponential function using function notation to represent the situation.
s(x)=(50)2^n-1
Because this function is about Summer trying to beat Jessie, it is appropriate to name this function s. Using the universal formula for writing an explicit formula for a geometric sequence, we come up with this function. The universal formula is an=a1r^n-1, where r is the common ratio.
_ Evaluate the function for inputs in the domain based on the context of the scenario.
Based on the scenario, the number of weeks is substituted by x. Lets say Summer wants to know how many pages she will have to read at on the 20th week. We simply plug in 20 wherever there is an x:
s(x)=(50)2^n-1
s(20)=(50)2^20-1
s(20)=(50)2^19
s(20)=(50)524,288
s(20)=26,214,400
By plugging in 20 (weeks) to the function, Summer now knows that she will have to read 26,214,400 pages on the 20th week. This is far-fetched, but she is still willing to stick to the plan. She can now figure out the amount of pages she will have to read for any given week, simply by plugging in the number she wishes to plug in.
_Write a recursive formula for this scenario.
t1=50
tn=(tn-1)2
s(x)=(50)2^n-1
Because this function is about Summer trying to beat Jessie, it is appropriate to name this function s. Using the universal formula for writing an explicit formula for a geometric sequence, we come up with this function. The universal formula is an=a1r^n-1, where r is the common ratio.
_ Evaluate the function for inputs in the domain based on the context of the scenario.
Based on the scenario, the number of weeks is substituted by x. Lets say Summer wants to know how many pages she will have to read at on the 20th week. We simply plug in 20 wherever there is an x:
s(x)=(50)2^n-1
s(20)=(50)2^20-1
s(20)=(50)2^19
s(20)=(50)524,288
s(20)=26,214,400
By plugging in 20 (weeks) to the function, Summer now knows that she will have to read 26,214,400 pages on the 20th week. This is far-fetched, but she is still willing to stick to the plan. She can now figure out the amount of pages she will have to read for any given week, simply by plugging in the number she wishes to plug in.
_Write a recursive formula for this scenario.
t1=50
tn=(tn-1)2