Analyzing Linear and Exponential Functions
-Create a linear function expressed symbolically. Then graph it.
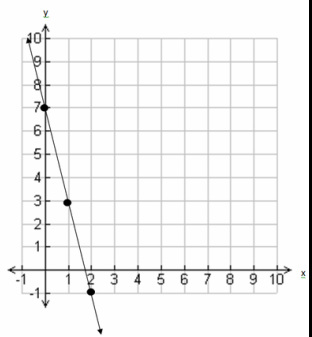
f(x)=-4x+7
f(x)=-4x+7
Because the graph has a negative slope of 4, the graphed line slopes downward. Since the function modeled has a y-intercept of positive 7, the line meets the y axis at (0,7).
-Create an exponential function expressed symbolically. Then graph it.
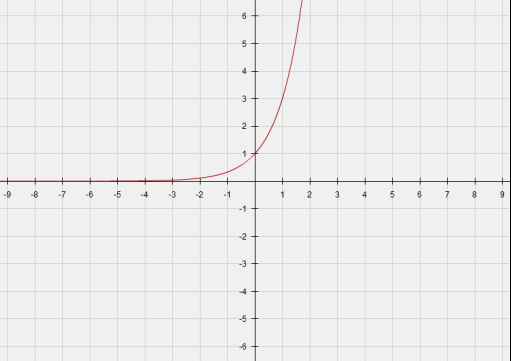
f(x)=3^x
f(x)=3^x
The graph curves because the terms in the range triple from one term to the next.
-Create a linear function and present it algebraically.
f(x)=5x+10
-Create a linear function and present it verbally.
f evaluated at x equals negative seven x minus four
-Compare the two functions.
For starters, the function I verbally described had a negative slope, so that specific line will slant downwards, while the one I algebraically described has a positive slope, so the line will slant upwards. The one I verbally described has a negative y-intercept. The line will cross the y axis below the x axis. The one I algebraically described has a positive y-intercept, therefore it's line will cross the y axis above the x axis. They are both examples of a LINEAR function.